今回から線形写像をテーマにして解説します。
線形写像は抽象度は高いですが、身につければ線形代数に対する理解が大きく深まると思います。
初回である今回の記事では、線形写像を学ぶ前段階として写像について解説していきます。
写像と像
集合$X$の元に対して、集合$Y$の元を定める対応$f$のことを写像といいます。
この時の$X$を定義域、$Y$を地域といいます。写像$f:X \to Y$によって$X$の元$x$に$Y$の元$y$が対応するとき、$y$を$f$による$x$の像といいます。
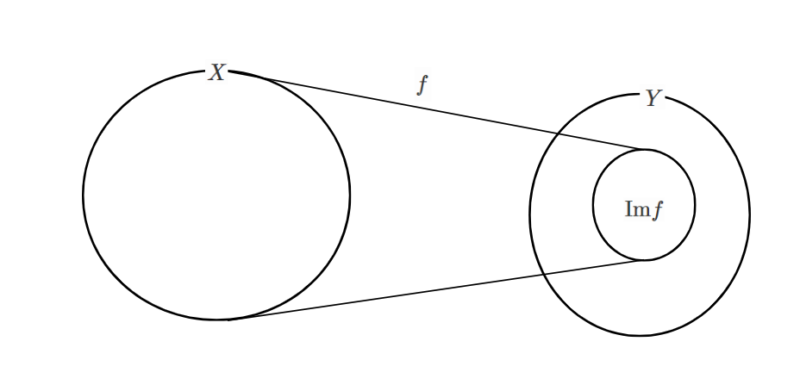
集合$X$のすべての元$x$に対応する像$f(x)$をまとめてできる集合を、集合$S$の$f$による像といい、$\mathrm{Im}f$または$f(X)$と表す。$\mathrm{Im}f$は集合$Y$の部分集合である。
$f(x)$と表すので、関数を思い浮かべると思いますが、実際高校で習った関数は実数集合から実数集合への写像と言うことが出来ます。
なお、写像はある元の$x$に対して$f(x)$がただ一つ定まるということが前提です。
例えば、$f(1)=3,6$のような対応は写像ではありません。
全射と単射
全射と単射はそれぞれ先ほど説明した写像の特別な場合の写像です。
全射
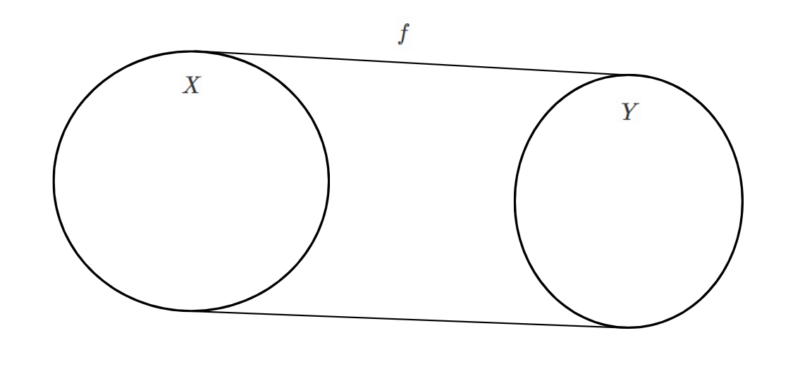
集合$Y$のすべての元が、集合$X$に含まれる何らかの元に対応するときの写像を全射といいます。
全射では、$\mathrm{Im}f=Y$が成り立ちます。
単射
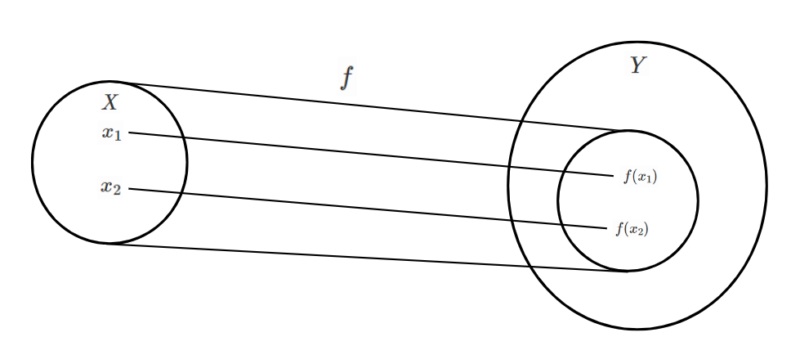
集合$X$の任意の異なる元$x_1,x_2$に対して、$f(x_1) \neq f(x_2)$が成り立つとき単射といいます。
すなわち、$x_1 \neq x_2$ならば、$f(x_1) \neq f(x_2)$です。
全単射
全射でありかつ単射でもある写像を全単射といいます。
写像の合成
写像も関数と同様に合成することができます。
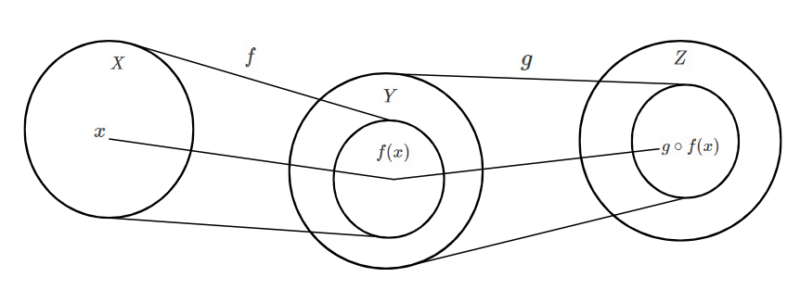
3つの集合$X,Y,Z$があり、写像$f:X \to Y$と写像$g:Y \to Z$を定義する。このとき集合$X$から集合$Z$への写像を$f$と$g$の合成写像といい、$g\circ f$と表す。
まとめ
今回は写像の定義、全射、単射、合成について解説しました。
写像はある集合の元を別の集合の元に変換する対応のことで、関数と似ています。
次回はいよいよ線形写像について解説していきます。










コメント